写算法时,需要在 时间 和 空间 之间做平衡(有时用空间换时间,有时用时间换空间)。
但这种思路没有考虑具体执行的实际情况,我们有可能写了一个看起来很优美的程序,但实际上狗屁不通,根本跑不起来。 因此,有必要对程序进行可观测性量化分析,通过时间综合检验程序的正确性。
我提出了”时间序列复杂度”和”单位时间序列复杂度”概念,试图补齐衡量算法效益的”最后一公里”。
传统时间空间复杂度
时间复杂度(Time Complexity)描述的是:算法执行所需的时间与输入规模之间的关系。
一般来说,O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(2^n) < O(n!)
空间复杂度(Space Complexity)描述的是:算法执行过程中所需内存空间与输入规模之间的关系。 它主要反映了算法对内存资源的消耗。
常见空间复杂度:
- O(1):只使用常数个额外变量,例如交换两个数。
- O(n):需要开辟与输入规模等长的数组,比如 BFS 队列。
- O(n^2):存储二维矩阵。
- O(n \log n):归并排序时的辅助数组。
- O(n!):存储所有排列结果。
时间序列复杂度
时间序列复杂度(Time Series Complexity)描述的是:在满足时间复杂度以及空间复杂度的前置性论述下,算法执行的实际时间以及内存资源的利用效率。
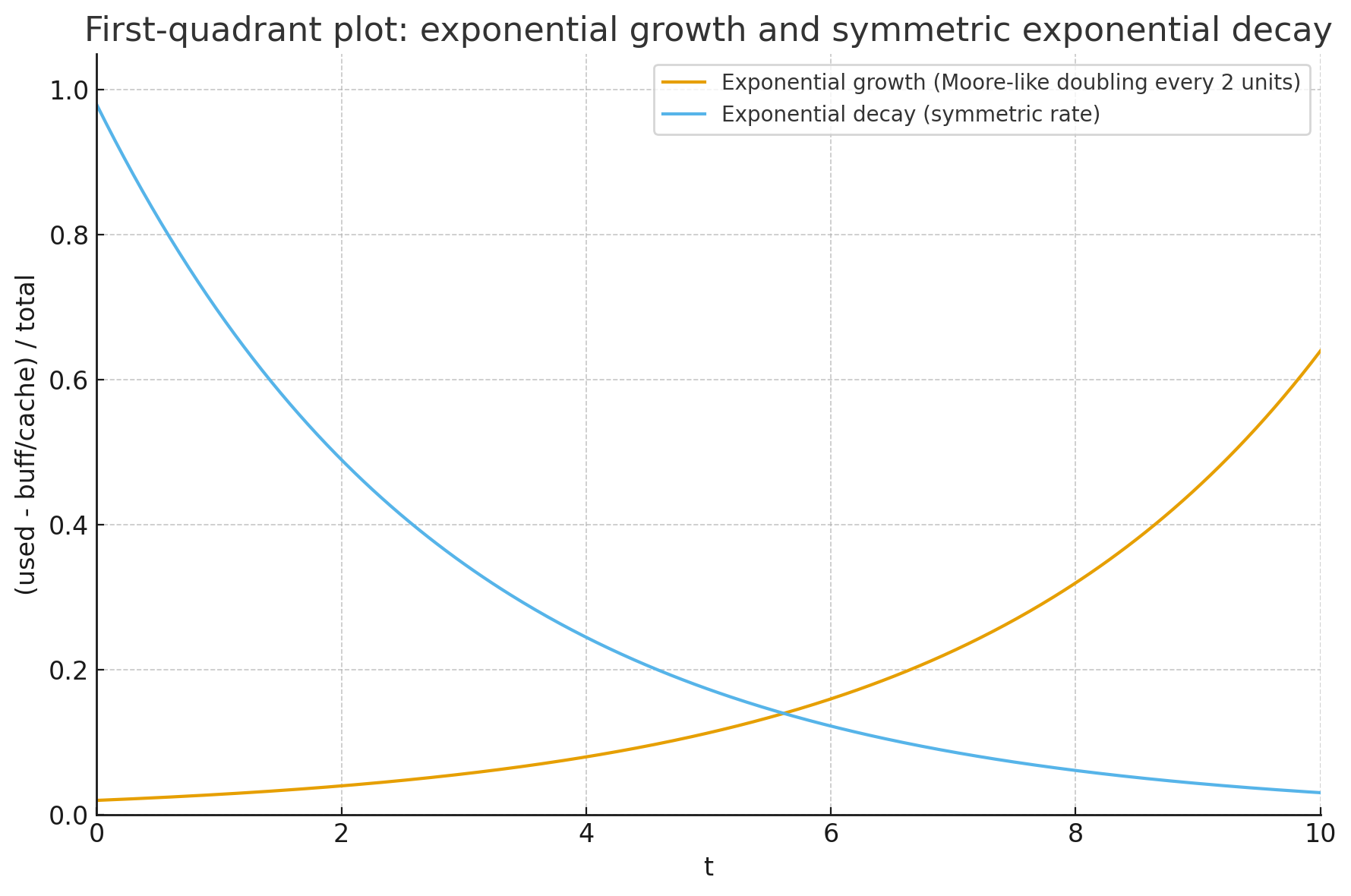
时间序列复杂度是一个二维图表。X轴是t,Y轴是(used - buff/cache) / total
时间序列复杂度需要对程序进行可观测性分析。个人比较喜欢指数衰减型。
//oracle:画一个二维坐标系,横轴是t,Y轴是(used - buff/cache) / total ,只需要第一象限,包含指数增长模拟摩尔定律的例子,以及相对称指数衰减图表。
O(1) “AI”
时间序列复杂度的这一概念,破除了传统时间空间算法复杂度的浅层优劣问题。说点人话,你可以用一个看起来很傻帽的程序去模拟AI,只要这个”AI”能骗到人(通过图灵测试)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
package main
import "fmt"
func main() {
fmt.Println("你:嗨,AI,你好吗?")
aiReply("嗨,AI,你好吗?")
}
func aiReply(input string) {
if input == "嗨,AI,你好吗?" {
fmt.Println("AI:我很好,谢谢你!你呢?")
if true { // 人继续问
fmt.Println("你:我也不错,你会讲笑话吗?")
if true { // AI 回答
fmt.Println("AI:当然,会的!你想听一个冷笑话还是热笑话?")
if true { // 人选择
fmt.Println("你:给我一个冷笑话吧。")
if true { // AI 输出
fmt.Println("AI:为什么计算机很冷?因为它总是在处理冷数据!")
if true { // 人继续
fmt.Println("你:哈哈,还有吗?")
if true {
fmt.Println("AI:还有啊,为什么AI不喜欢夏天?因为它怕被训练成热模型!")
if true {
fmt.Println("你:太好笑了,你会自己讲笑话吗?")
if true {
fmt.Println("AI:嗯……让我想想……你知道程序员最怕的是什么吗?")
if true {
fmt.Println("你:是什么?")
if true {
fmt.Println("AI:被无限循环困住!")
}
}
}
}
}
}
}
}
}
}
}
}
这个程序按照传统时间空间算法去计算,都是O(1)。
或者换一种思路,你可以用一台十年前的安卓机去证明自己,也可以找你爸要一个亿,买一台带超强GPU的至强服务器,去算1+1=2。这就是一种个人选择,无关乎对错问题。
伪AI电话
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
package main
import (
"fmt"
"time"
)
// 固定的话术脚本
var script = []string{
"您好,这里是XX银行智能客服中心。",
"我们最近推出了一款超低利率的信用贷款产品,年利率低至3.5%。",
"无需抵押,最快30分钟即可放款,非常适合资金周转。",
"请问您现在是否需要了解一下具体的办理流程呢?",
"我们可以根据您的个人情况,提供最高50万的额度支持。",
"办理过程全程在线,非常简单方便。",
"如果您有兴趣,我可以帮您安排专属客户经理与您联系。",
"感谢您的来电,希望我们的贷款产品能帮到您!",
}
func fakeLoanCall() {
fmt.Println("📞 电话拨号中...")
time.Sleep(time.Second * 2)
fmt.Println("AI:嘟嘟嘟……接通成功!")
for _, line := range script {
time.Sleep(time.Second * 2)
fmt.Println("AI:", line)
// 模拟用户反应
time.Sleep(time.Second)
fmt.Println("你:嗯……好的。")
}
fmt.Println("📞 通话结束,感谢使用伪AI电话营销系统。")
}
func main() {
fakeLoanCall()
}
📞 电话拨号中...
AI:嘟嘟嘟……接通成功!
AI: 您好,这里是XX银行智能客服中心。
你: 嗯……好的。
AI: 我们最近推出了一款超低利率的信用贷款产品,年利率低至3.5%。
你: 嗯……好的。
AI: 无需抵押,最快30分钟即可放款,非常适合资金周转。
你: 嗯……好的。
AI: 请问您现在是否需要了解一下具体的办理流程呢?
你: 嗯……好的。
AI: 我们可以根据您的个人情况,提供最高50万的额度支持。
你: 嗯……好的。
AI: 办理过程全程在线,非常简单方便。
你: 嗯……好的。
AI: 如果您有兴趣,我可以帮您安排专属客户经理与您联系。
你: 嗯……好的。
AI: 感谢您的来电,希望我们的贷款产品能帮到您!
你: 嗯……好的。
📞 通话结束,感谢使用伪AI电话营销系统。
很多学计算机的书呆子,喜欢按照传统计算机的定义去思考分析问题。但他们没有认识到问题的本身来源于生活。
因此,通过蜉蝣交配这个非常简单的例子,就能解答”时间序列复杂度”这一概念。
蜉蝣的空中交配
抓握:雄性成功接近雌性后,会用其细长的前足紧紧抓住雌性的胸部。
体位调整:雄性然后弯曲其腹部末端长长的抱握器,牢牢地箍住雌性的腹部末端。
连接:此时,两只蜉蝣呈现”雄上雌下”的 tandem position(串联姿势),共同飞行。
授精:在连接飞行中,雄性的阴茎会与雌性的受精囊孔对接,将精包(精囊)注入雌性体内。整个交配过程完全在飞行中完成,持续时间从几秒到几分钟不等。
单位时间序列复杂度
单位时间序列复杂度(Unit Time Series Complexity)是一种复合衡量算法效率的细化公式。 在内存的基础上按需加入CPU/GPU。 用来衡量算法单位资源使用效率。
单位时间序列复杂度是一个三维图表。 不过三维图表过于抽象,一般是降维成2个2维图表。或者合并Y轴,变成一个二维图表的两条曲线。
单位CPU时间序列复杂度(Unit CPU Time Series Complexity)
单位CPU时间序列复杂度是一个三维图表。
X轴是t,
Y轴是(used - buff/cache) / total,
Z轴是cpu_load1。
也可以按需替换成load5和load15。
- cpu_load1:过去 1 分钟的平均负载
- cpu_load5:过去 5 分钟的平均负载
- cpu_load15:过去 15 分钟的平均负载
单位GPU时间序列复杂度(Unit GPU Time Series Complexity)
单位GPU时间序列复杂度是一个三维图表。
X轴是t,
Y轴是(used - buff/cache) / total,
Z轴是gpu_utilization。
或者把 gpu_utilization 换成 gpu_memory_utilization。
P学:3秒真男人
假设TA只有3秒就没了,那么这个函数的横轴区间就是[0,3],0是相对的瞬时概念,表示”现在”。
3秒后,free -m 就归零了,表示”一滴都不剩”了。
单纯从时间角度分析,蜉蝣的交配过程可谓是相当效率。但如果把它换成我的好邻居,那我一般建议他们去看一下男科。
如果他们对象不是很丑的话,我可以考虑顺便照顾一下。

拓展
Y轴可以换成单位能耗指标,用来规划建设节能型智慧建筑。
与其说纵轴是内存利用率,不如说纵轴表示一种资源的利用效率。
让我们看看摩尔定律的极限到底在哪里吧。
结论
大鹏展翅恨天低
When writing algorithms, we need to balance between time and space (sometimes trading space for time, sometimes trading time for space).

But this thinking doesn’t consider the actual execution situation. We might write a program that looks beautiful, but actually makes no sense and can’t run at all. Therefore, it’s necessary to perform observable quantitative analysis on programs, comprehensively testing program correctness through time.
I propose the concepts of “Time Series Complexity” and “Unit Time Series Complexity” to try to complete the “last mile” of measuring algorithm efficiency.
Traditional Time and Space Complexity
Time Complexity describes the relationship between the time required for algorithm execution and the input size.
Generally speaking, O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(2^n) < O(n!)
Space Complexity describes the relationship between the memory space required during algorithm execution and the input size. It mainly reflects the algorithm’s consumption of memory resources.
Common space complexities:
- O(1): Only uses a constant number of additional variables, e.g., swapping two numbers.
- O(n): Needs to allocate an array equal in length to the input size, like a BFS queue.
- O(n^2): Storing a two-dimensional matrix.
- O(n \log n): Auxiliary array during merge sort.
- O(n!): Storing all permutation results.
Time Series Complexity
Time Series Complexity describes: under the premise of satisfying time complexity and space complexity, the actual time of algorithm execution and the utilization efficiency of memory resources.
Time Series Complexity is a two-dimensional chart. The X-axis is t, and the Y-axis is (used - buff/cache) / total
Time Series Complexity requires observable analysis of programs. Personally, I prefer exponential decay type.
//oracle: Draw a two-dimensional coordinate system, with the horizontal axis as t and the Y-axis as (used - buff/cache) / total, only the first quadrant is needed, including examples of exponential growth simulating Moore’s Law, and corresponding exponential decay charts.

O(1) “AI”
This concept of Time Series Complexity breaks through the shallow advantages and disadvantages of traditional time-space algorithm complexity. In plain language, you can use a program that looks silly to simulate AI, as long as this “AI” can fool people (pass the Turing test).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
package main
import "fmt"
func main() {
fmt.Println("You: Hi, AI, how are you?")
aiReply("Hi, AI, how are you?")
}
func aiReply(input string) {
if input == "Hi, AI, how are you?" {
fmt.Println("AI: I'm fine, thank you! How about you?")
if true { // Person continues asking
fmt.Println("You: I'm good too, can you tell jokes?")
if true { // AI answers
fmt.Println("AI: Of course! Would you like to hear a cold joke or a hot joke?")
if true { // Person chooses
fmt.Println("You: Give me a cold joke.")
if true { // AI outputs
fmt.Println("AI: Why is the computer cold? Because it's always processing cold data!")
if true { // Person continues
fmt.Println("You: Haha, any more?")
if true {
fmt.Println("AI: Yes, why doesn't AI like summer? Because it's afraid of being trained into a hot model!")
if true {
fmt.Println("You: So funny, can you tell jokes yourself?")
if true {
fmt.Println("AI: Hmm... let me think... Do you know what programmers fear most?")
if true {
fmt.Println("You: What is it?")
if true {
fmt.Println("AI: Being trapped in an infinite loop!")
}
}
}
}
}
}
}
}
}
}
}
}
This program, calculated according to traditional time-space algorithms, is O(1).
Or think of it another way: you can use a ten-year-old Android phone to prove yourself, or ask your dad for a hundred million to buy a Xeon server with super powerful GPU to calculate 1+1=2. This is a personal choice, not a matter of right or wrong.
Fake AI Phone Call
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
package main
import (
"fmt"
"time"
)
// Fixed script
var script = []string{
"Hello, this is XX Bank Intelligent Customer Service Center.",
"We recently launched an ultra-low interest rate credit loan product with an annual interest rate as low as 3.5%.",
"No collateral required, funds can be released in as fast as 30 minutes, very suitable for capital turnover.",
"Would you like to learn about the specific application process?",
"We can provide up to 500,000 in credit support based on your personal situation.",
"The entire application process is online, very simple and convenient.",
"If you're interested, I can arrange a dedicated account manager to contact you.",
"Thank you for your call, we hope our loan product can help you!",
}
func fakeLoanCall() {
fmt.Println("📞 Dialing...")
time.Sleep(time.Second * 2)
fmt.Println("AI: Beep beep beep... Connection successful!")
for _, line := range script {
time.Sleep(time.Second * 2)
fmt.Println("AI:", line)
// Simulate user response
time.Sleep(time.Second)
fmt.Println("You: Um... okay.")
}
fmt.Println("📞 Call ended, thank you for using the fake AI phone marketing system.")
}
func main() {
fakeLoanCall()
}
📞 Dialing...
AI: Beep beep beep... Connection successful!
AI: Hello, this is XX Bank Intelligent Customer Service Center.
You: Um... okay.
AI: We recently launched an ultra-low interest rate credit loan product with an annual interest rate as low as 3.5%.
You: Um... okay.
AI: No collateral required, funds can be released in as fast as 30 minutes, very suitable for capital turnover.
You: Um... okay.
AI: Would you like to learn about the specific application process?
You: Um... okay.
AI: We can provide up to 500,000 in credit support based on your personal situation.
You: Um... okay.
AI: The entire application process is online, very simple and convenient.
You: Um... okay.
AI: If you're interested, I can arrange a dedicated account manager to contact you.
You: Um... okay.
AI: Thank you for your call, we hope our loan product can help you!
You: Um... okay.
📞 Call ended, thank you for using the fake AI phone marketing system.
Many computer nerds like to think and analyze problems according to traditional computer definitions. But they don’t recognize that problems themselves come from life.
Therefore, through the very simple example of mayfly mating, we can explain the concept of “Time Series Complexity”.
Mayfly Aerial Mating
Grasping: After the male successfully approaches the female, he uses his slender forelegs to tightly grasp the female’s thorax.
Position adjustment: The male then bends the long claspers at the end of his abdomen to firmly clamp the end of the female’s abdomen.
Connection: At this point, the two mayflies present a “male on top, female below” tandem position, flying together.
Insemination: During connected flight, the male’s penis connects with the female’s spermathecal opening, injecting the spermatophore (sperm sac) into the female’s body. The entire mating process is completed entirely in flight, lasting from a few seconds to several minutes.
Unit Time Series Complexity
Unit Time Series Complexity is a refined formula for composite measurement of algorithm efficiency. On the basis of memory, CPU/GPU is added as needed. Used to measure algorithm unit resource utilization efficiency.
Unit Time Series Complexity is a three-dimensional chart. However, three-dimensional charts are too abstract, generally reduced to 2 two-dimensional charts. Or merge the Y-axis to become two curves in a two-dimensional chart.
Unit CPU Time Series Complexity
Unit CPU Time Series Complexity is a three-dimensional chart.
X-axis is t,
Y-axis is (used - buff/cache) / total,
Z-axis is cpu_load1.
Can also be replaced with load5 and load15 as needed.
- cpu_load1: Average load over the past 1 minute
- cpu_load5: Average load over the past 5 minutes
- cpu_load15: Average load over the past 15 minutes
Unit GPU Time Series Complexity
Unit GPU Time Series Complexity is a three-dimensional chart.
X-axis is t,
Y-axis is (used - buff/cache) / total,
Z-axis is gpu_utilization.
Or replace gpu_utilization with gpu_memory_utilization.
P Theory: 3-Second Real Man

Assuming TA only has 3 seconds, then the horizontal axis interval of this function is [0,3], where 0 is a relative instantaneous concept, representing “now”.
After 3 seconds, free -m returns to zero, meaning “not a drop left”.
From a pure time perspective, the mayfly’s mating process is quite efficient. But if we replace it with my good neighbor, I generally suggest they see a urologist.
If their partner isn’t too ugly, I might consider taking care of them as well.

Extension
The Y-axis can be replaced with unit energy consumption indicators, used to plan and construct energy-saving smart buildings.
Rather than saying the vertical axis is memory utilization, it’s better to say the vertical axis represents the utilization efficiency of a resource.
Let’s see where the limits of Moore’s Law really are.
Conclusion
The great peng spreads its wings, hating the sky is too low
アルゴリズムを書くとき、時間と空間の間でバランスを取る必要があります(時には空間を時間と交換し、時には時間を空間と交換します)。

しかし、この考え方は実際の実行状況を考慮していません。美しく見えるプログラムを書いたかもしれませんが、実際には意味がなく、まったく実行できません。 したがって、プログラムに対して観測可能な定量的分析を実行し、時間を通じてプログラムの正確性を総合的にテストする必要があります。
アルゴリズム効率を測定する「最後の1キロメートル」を完成させるために、「時系列複雑度」と「単位時系列複雑度」の概念を提案します。
従来の時間空間複雑度
時間複雑度(Time Complexity)は、アルゴリズムの実行に必要な時間と入力サイズの関係を記述します。
一般的に、O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(2^n) < O(n!)
空間複雑度(Space Complexity)は、アルゴリズムの実行中に必要なメモリ空間と入力サイズの関係を記述します。 主にアルゴリズムのメモリリソースの消費を反映します。
一般的な空間複雑度:
- O(1):定数の追加変数のみを使用、例:2つの数値を交換
- O(n):入力サイズと同じ長さの配列を割り当てる必要がある、例:BFSキュー
- O(n^2):2次元行列を格納
- O(n \log n):マージソート時の補助配列
- O(n!):すべての順列結果を格納
時系列複雑度
時系列複雑度(Time Series Complexity)は、時間複雑度と空間複雑度を満たす前提の下で、アルゴリズムの実行の実際の時間とメモリリソースの利用効率を記述します。
時系列複雑度は2次元チャートです。X軸はt、Y軸は(used - buff/cache) / total
時系列複雑度は、プログラムの観測可能な分析を必要とします。個人的には指数減衰型を好みます。
//oracle: 2次元座標系を描画し、横軸をt、Y軸を(used - buff/cache) / totalとし、第1象限のみが必要で、ムーアの法則をシミュレートする指数成長の例と、対応する指数減衰チャートを含む。

O(1)「AI」
時系列複雑度のこの概念は、従来の時間空間アルゴリズム複雑度の浅い優劣の問題を突破します。わかりやすく言えば、愚かに見えるプログラムを使用してAIをシミュレートできます。この「AI」が人を騙すことができる限り(チューリングテストに合格)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
package main
import "fmt"
func main() {
fmt.Println("あなた:こんにちは、AI、元気ですか?")
aiReply("こんにちは、AI、元気ですか?")
}
func aiReply(input string) {
if input == "こんにちは、AI、元気ですか?" {
fmt.Println("AI:元気です、ありがとう!あなたは?")
if true { // 人が続けて尋ねる
fmt.Println("あなた:私も元気です、ジョークを言えますか?")
if true { // AIが答える
fmt.Println("AI:もちろん!冷たいジョークと熱いジョーク、どちらを聞きたいですか?")
if true { // 人が選択
fmt.Println("あなた:冷たいジョークをください。")
if true { // AIが出力
fmt.Println("AI:なぜコンピュータは冷たいのですか?常に冷たいデータを処理しているからです!")
if true { // 人が続ける
fmt.Println("あなた:ハハ、他には?")
if true {
fmt.Println("AI:はい、なぜAIは夏が嫌いなのですか?ホットモデルに訓練されることを恐れているからです!")
if true {
fmt.Println("あなた:とても面白い、自分でジョークを言えますか?")
if true {
fmt.Println("AI:うーん……考えさせてください……プログラマーが最も恐れるものは何だと思いますか?")
if true {
fmt.Println("あなた:何ですか?")
if true {
fmt.Println("AI:無限ループに閉じ込められること!")
}
}
}
}
}
}
}
}
}
}
}
}
このプログラムは、従来の時間空間アルゴリズムに従って計算すると、O(1)です。
または別の考え方として、10年前のAndroid携帯電話を使用して自分を証明することも、お父さんに10億円を求めて超強力なGPUを搭載したXeonサーバーを購入し、1+1=2を計算することもできます。これは個人的な選択であり、正誤の問題ではありません。
偽AI電話
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
package main
import (
"fmt"
"time"
)
// 固定スクリプト
var script = []string{
"こんにちは、こちらはXX銀行インテリジェントカスタマーサービスセンターです。",
"最近、年利3.5%という超低金利の信用ローン商品を発売しました。",
"担保不要、最短30分で融資可能、資金繰りに最適です。",
"具体的な申請プロセスについて知りたいですか?",
"お客様の個人状況に応じて、最高50万円の信用枠を提供できます。",
"申請プロセス全体がオンラインで、非常にシンプルで便利です。",
"ご興味があれば、専属のアカウントマネージャーを手配して連絡させることができます。",
"お電話ありがとうございました。当社のローン商品がお役に立てれば幸いです!",
}
func fakeLoanCall() {
fmt.Println("📞 ダイヤル中...")
time.Sleep(time.Second * 2)
fmt.Println("AI:ピーピーピー……接続成功!")
for _, line := range script {
time.Sleep(time.Second * 2)
fmt.Println("AI:", line)
// ユーザーの反応をシミュレート
time.Sleep(time.Second)
fmt.Println("あなた:うーん……わかりました。")
}
fmt.Println("📞 通話終了、偽AI電話マーケティングシステムをご利用いただきありがとうございました。")
}
func main() {
fakeLoanCall()
}
📞 ダイヤル中...
AI:ピーピーピー……接続成功!
AI: こんにちは、こちらはXX銀行インテリジェントカスタマーサービスセンターです。
あなた: うーん……わかりました。
AI: 最近、年利3.5%という超低金利の信用ローン商品を発売しました。
あなた: うーん……わかりました。
AI: 担保不要、最短30分で融資可能、資金繰りに最適です。
あなた: うーん……わかりました。
AI: 具体的な申請プロセスについて知りたいですか?
あなた: うーん……わかりました。
AI: お客様の個人状況に応じて、最高50万円の信用枠を提供できます。
あなた: うーん……わかりました。
AI: 申請プロセス全体がオンラインで、非常にシンプルで便利です。
あなた: うーん……わかりました。
AI: ご興味があれば、専属のアカウントマネージャーを手配して連絡させることができます。
あなた: うーん……わかりました。
AI: お電話ありがとうございました。当社のローン商品がお役に立てれば幸いです!
あなた: うーん……わかりました。
📞 通話終了、偽AI電話マーケティングシステムをご利用いただきありがとうございました。
多くのコンピュータオタクは、従来のコンピュータの定義に従って問題を考え、分析することを好みます。しかし、問題自体が生活から来ていることを認識していません。
したがって、カゲロウの交配という非常に簡単な例を通じて、「時系列複雑度」の概念を説明できます。
カゲロウの空中交配
把握:オスがメスに成功して接近した後、細長い前足を使用してメスの胸部をしっかりと把握します。
体位調整:オスはその後、腹部の端にある長い把握器を曲げ、メスの腹部の端をしっかりと固定します。
接続:この時点で、2匹のカゲロウは「オスが上、メスが下」のタンデムポジションを呈し、一緒に飛行します。
授精:接続飛行中、オスのペニスがメスの受精嚢孔に接続し、精包(精嚢)をメスの体内に注入します。交配プロセス全体が完全に飛行中に完了し、数秒から数分まで続きます。
単位時系列複雑度
単位時系列複雑度(Unit Time Series Complexity)は、アルゴリズム効率を複合測定する細分化された公式です。 メモリの基礎の上に、必要に応じてCPU/GPUを追加します。 アルゴリズムの単位リソース利用効率を測定するために使用されます。
単位時系列複雑度は3次元チャートです。 ただし、3次元チャートは抽象的すぎるため、一般に2つの2次元チャートに次元削減されます。またはY軸をマージして、2次元チャートの2つの曲線にします。
単位CPU時系列複雑度
単位CPU時系列複雑度は3次元チャートです。
X軸はt、
Y軸は(used - buff/cache) / total、
Z軸はcpu_load1。
必要に応じてload5とload15に置き換えることもできます。
- cpu_load1:過去1分間の平均負荷
- cpu_load5:過去5分間の平均負荷
- cpu_load15:過去15分間の平均負荷
単位GPU時系列複雑度
単位GPU時系列複雑度は3次元チャートです。
X軸はt、
Y軸は(used - buff/cache) / total、
Z軸はgpu_utilization。
またはgpu_utilizationをgpu_memory_utilizationに置き換えることもできます。
P学:3秒の真の男

TAが3秒しかないと仮定すると、この関数の横軸の区間は[0,3]で、0は相対的な瞬間的な概念で、「今」を表します。
3秒後、free -mはゼロに戻り、「一滴も残っていない」ことを意味します。
純粋に時間の観点から分析すると、カゲロウの交配プロセスは非常に効率的です。しかし、私の良い隣人に置き換えると、一般的に泌尿器科に行くことをお勧めします。
彼らのパートナーがあまり醜くない場合、私も一緒に世話を検討できます。

拡張
Y軸は単位エネルギー消費指標に置き換えることができ、省エネ型スマートビルの計画と建設に使用されます。
縦軸がメモリ利用率であると言うよりも、縦軸がリソースの利用効率を表すと言う方が適切です。
ムーアの法則の限界がどこにあるかを見てみましょう。
結論
大鵬が翼を広げ、空が低すぎることを恨む
При написании алгоритмов необходимо балансировать между временем и пространством (иногда обменивая пространство на время, иногда время на пространство).

Но это мышление не учитывает фактическую ситуацию выполнения. Мы можем написать программу, которая выглядит красиво, но на самом деле не имеет смысла и вообще не может работать. Поэтому необходимо провести наблюдаемый количественный анализ программ, комплексно проверяя правильность программ через время.
Я предлагаю концепции “Временная сложность ряда” и “Единичная временная сложность ряда”, чтобы попытаться завершить “последний километр” измерения эффективности алгоритмов.
Традиционная временная и пространственная сложность
Временная сложность (Time Complexity) описывает связь между временем, необходимым для выполнения алгоритма, и размером входа.
Обычно O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(2^n) < O(n!)
Пространственная сложность (Space Complexity) описывает связь между пространством памяти, необходимым во время выполнения алгоритма, и размером входа. Она в основном отражает потребление алгоритмом ресурсов памяти.
Общие пространственные сложности:
- O(1): Использует только постоянное количество дополнительных переменных, например, обмен двух чисел.
- O(n): Нужно выделить массив равной длины размеру входа, например, очередь BFS.
- O(n^2): Хранение двумерной матрицы.
- O(n \log n): Вспомогательный массив при сортировке слиянием.
- O(n!): Хранение всех результатов перестановок.
Временная сложность ряда
Временная сложность ряда (Time Series Complexity) описывает: при условии удовлетворения временной сложности и пространственной сложности, фактическое время выполнения алгоритма и эффективность использования ресурсов памяти.
Временная сложность ряда — это двумерный график. Ось X — это t, ось Y — это (used - buff/cache) / total
Временная сложность ряда требует наблюдаемого анализа программ. Лично я предпочитаю экспоненциальный тип затухания.
//oracle: Нарисовать двумерную систему координат, с горизонтальной осью t и осью Y (used - buff/cache) / total, нужен только первый квадрант, включая примеры экспоненциального роста, моделирующие закон Мура, и соответствующие графики экспоненциального затухания.

O(1) “AI”
Эта концепция временной сложности ряда прорывается через поверхностные преимущества и недостатки традиционной временно-пространственной сложности алгоритмов. Простыми словами, вы можете использовать программу, которая выглядит глупо, чтобы симулировать AI, пока этот “AI” может обмануть людей (пройти тест Тьюринга).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
package main
import "fmt"
func main() {
fmt.Println("Вы: Привет, AI, как дела?")
aiReply("Привет, AI, как дела?")
}
func aiReply(input string) {
if input == "Привет, AI, как дела?" {
fmt.Println("AI: У меня все хорошо, спасибо! А у вас?")
if true { // Человек продолжает спрашивать
fmt.Println("Вы: У меня тоже хорошо, умеете рассказывать шутки?")
if true { // AI отвечает
fmt.Println("AI: Конечно! Хотите услышать холодную шутку или горячую шутку?")
if true { // Человек выбирает
fmt.Println("Вы: Дайте мне холодную шутку.")
if true { // AI выводит
fmt.Println("AI: Почему компьютер холодный? Потому что он всегда обрабатывает холодные данные!")
if true { // Человек продолжает
fmt.Println("Вы: Ха-ха, еще есть?")
if true {
fmt.Println("AI: Да, почему AI не любит лето? Потому что боится быть обученным в горячую модель!")
if true {
fmt.Println("Вы: Так смешно, умеете сами рассказывать шутки?")
if true {
fmt.Println("AI: Хм... дайте подумать... Знаете, чего программисты боятся больше всего?")
if true {
fmt.Println("Вы: Чего?")
if true {
fmt.Println("AI: Быть запертыми в бесконечном цикле!")
}
}
}
}
}
}
}
}
}
}
}
}
Эта программа, рассчитанная по традиционным временно-пространственным алгоритмам, имеет O(1).
Или подумайте по-другому: вы можете использовать десятилетний Android-телефон, чтобы доказать себя, или попросить у папы сто миллионов, чтобы купить сервер Xeon с супермощным GPU для вычисления 1+1=2. Это личный выбор, не вопрос правильности или неправильности.
Поддельный AI-звонок
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
package main
import (
"fmt"
"time"
)
// Фиксированный сценарий
var script = []string{
"Здравствуйте, это интеллектуальный центр обслуживания клиентов банка XX.",
"Мы недавно запустили продукт кредита с ультранизкой процентной ставкой с годовой процентной ставкой всего 3.5%.",
"Без залога, средства могут быть выданы в течение 30 минут, очень подходит для оборота капитала.",
"Хотели бы вы узнать о конкретном процессе подачи заявки?",
"Мы можем предоставить до 500,000 кредитной поддержки на основе вашей личной ситуации.",
"Весь процесс подачи заявки проходит онлайн, очень просто и удобно.",
"Если вы заинтересованы, я могу организовать для вас связь с персональным менеджером по счетам.",
"Спасибо за ваш звонок, мы надеемся, что наш кредитный продукт может помочь вам!",
}
func fakeLoanCall() {
fmt.Println("📞 Набор номера...")
time.Sleep(time.Second * 2)
fmt.Println("AI: Бип-бип-бип... Соединение успешно!")
for _, line := range script {
time.Sleep(time.Second * 2)
fmt.Println("AI:", line)
// Симулировать реакцию пользователя
time.Sleep(time.Second)
fmt.Println("Вы: Эм... хорошо.")
}
fmt.Println("📞 Звонок завершен, спасибо за использование поддельной системы AI-телефонного маркетинга.")
}
func main() {
fakeLoanCall()
}
📞 Набор номера...
AI: Бип-бип-бип... Соединение успешно!
AI: Здравствуйте, это интеллектуальный центр обслуживания клиентов банка XX.
Вы: Эм... хорошо.
AI: Мы недавно запустили продукт кредита с ультранизкой процентной ставкой с годовой процентной ставкой всего 3.5%.
Вы: Эм... хорошо.
AI: Без залога, средства могут быть выданы в течение 30 минут, очень подходит для оборота капитала.
Вы: Эм... хорошо.
AI: Хотели бы вы узнать о конкретном процессе подачи заявки?
Вы: Эм... хорошо.
AI: Мы можем предоставить до 500,000 кредитной поддержки на основе вашей личной ситуации.
Вы: Эм... хорошо.
AI: Весь процесс подачи заявки проходит онлайн, очень просто и удобно.
Вы: Эм... хорошо.
AI: Если вы заинтересованы, я могу организовать для вас связь с персональным менеджером по счетам.
Вы: Эм... хорошо.
AI: Спасибо за ваш звонок, мы надеемся, что наш кредитный продукт может помочь вам!
Вы: Эм... хорошо.
📞 Звонок завершен, спасибо за использование поддельной системы AI-телефонного маркетинга.
Многие компьютерные ботаники любят думать и анализировать проблемы согласно традиционным компьютерным определениям. Но они не осознают, что проблемы сами по себе происходят из жизни.
Поэтому через очень простой пример спаривания поденок мы можем объяснить концепцию “Временной сложности ряда”.
Воздушное спаривание поденок
Захват: После того, как самец успешно приближается к самке, он использует свои тонкие передние ноги, чтобы крепко схватить грудь самки.
Корректировка позиции: Самец затем сгибает длинные хватательные органы на конце брюшка, чтобы прочно зажать конец брюшка самки.
Соединение: В этот момент две поденки представляют тандемную позицию “самец сверху, самка снизу”, летя вместе.
Осеменение: Во время соединенного полета пенис самца соединяется с отверстием семяприемника самки, вводя сперматофор (семенной мешок) в тело самки. Весь процесс спаривания полностью завершается в полете, длится от нескольких секунд до нескольких минут.
Единичная временная сложность ряда
Единичная временная сложность ряда (Unit Time Series Complexity) — это уточненная формула для комплексного измерения эффективности алгоритмов. На основе памяти по необходимости добавляется CPU/GPU. Используется для измерения эффективности использования единичных ресурсов алгоритма.
Единичная временная сложность ряда — это трехмерный график. Однако трехмерные графики слишком абстрактны, обычно сводятся к 2 двумерным графикам. Или объединяют ось Y, превращаясь в две кривые в двумерном графике.
Единичная CPU временная сложность ряда
Единичная CPU временная сложность ряда — это трехмерный график.
Ось X — это t,
ось Y — это (used - buff/cache) / total,
ось Z — это cpu_load1.
Также можно заменить на load5 и load15 по необходимости.
- cpu_load1: Средняя нагрузка за последние 1 минуту
- cpu_load5: Средняя нагрузка за последние 5 минут
- cpu_load15: Средняя нагрузка за последние 15 минут
Единичная GPU временная сложность ряда
Единичная GPU временная сложность ряда — это трехмерный график.
Ось X — это t,
ось Y — это (used - buff/cache) / total,
ось Z — это gpu_utilization.
Или заменить gpu_utilization на gpu_memory_utilization.
P-теория: 3-секундный настоящий мужчина

Предполагая, что у TA есть только 3 секунды, то горизонтальный интервал этой функции [0,3], где 0 — это относительное мгновенное понятие, представляющее “сейчас”.
Через 3 секунды free -m возвращается к нулю, означая “не осталось ни капли”.
С чисто временной точки зрения, процесс спаривания поденок довольно эффективен. Но если заменить его на моего хорошего соседа, я обычно предлагаю им обратиться к урологу.
Если их партнер не слишком уродлив, я могу рассмотреть возможность позаботиться о них тоже.

Расширение
Ось Y может быть заменена показателями единичного энергопотребления, используемыми для планирования и строительства энергосберегающих умных зданий.
Скорее чем говорить, что вертикальная ось — это использование памяти, лучше сказать, что вертикальная ось представляет эффективность использования ресурса.
Давайте посмотрим, где действительно находятся пределы закона Мура.
Заключение
Великий пингвин расправляет крылья, ненавидя, что небо слишком низко